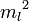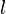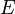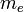Атом водорода - Математическое описание атома водорода

Химия - Атом водорода - Математическое описание атома водорода

01 марта 2011

Оглавление:
1. Атом водорода
2. Решение уравнения Шрёдингера
3. Математическое описание атома водорода
4. Визуализация орбиталей атома водорода
5. См

Энергетический спектр

Энергетические уровни атома водорода, включая тонкую структуру записываются в виде

$E_{nj} = \frac{E_0}{n^2} \left \right) \,$

где

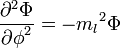$~\alpha$ — постоянная тонкой структуры

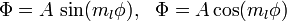$~j$ — собственное значение оператора полного момента импульса

Энергию 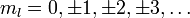$~E$ можно найти в простой модели Бора, с массой электрона 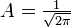$~m_e$ и зарядом электрона $~e_0$ :

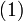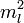
$~{E_0}=-{\frac{{m_e}{e_0^4}}{8{h^2}{{\varepsilon}_0^2}}}~{\approx}~13,62323824~{\rm{eV}}~{\approx}~{2,182700518{\times}10^{-18}~{\rm{J}}}$

где 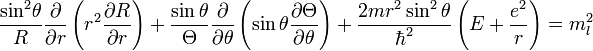$~{\rm{eV}}~-$ электронвольты, 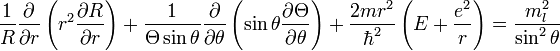$~{\rm{J}}~-$ джоули, 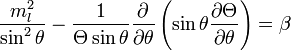$~h~-$ постоянная Планка, 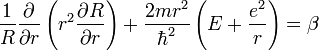$~{\varepsilon}_0~-$ диэлектрическая проницаемость вакуума.

Волновые функции

В сферических координатах волновые функции имеют вид:

$\psi_{nlm} = \sqrt {{\left}^3\frac{!}{2n^3} } {\cdot} \exp{ \left } {\cdot} {\left}^{l} L_{n+l}^{2l+1}{ \left} \cdot Y_{l,m}$

где:

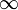$~{a_0}$ — Боровский радиус.

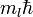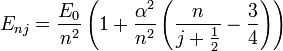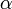$L_{n+l}^{2l+1}$ — обобщённые полиномы Лагерра степени $~{n+l}$ — функции от $~\frac{2r}{n a_0}$ .

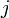$Y_{l,m} \,$ — сферические функции.

Угловой момент

Собственные значения для оператора углового момента:

$L^2 | n, l, m \rang = {\hbar}^2 l | n, l, m \rang$

$L_z | n, l, m \rang = \hbar m | n, l, m \rang$

Нахождение энергии электрона из модели Бора

Вычислим уровни энергии атома водорода без учета тонкой структуры, используя простую модель атома Бора. Для этой цели можно сделать грубое допущение электрона, двигающегося по круговой орбите на фиксированном расстоянии. Приравнивая кулоновскую силу притяжения 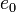$~\frac{e_0^2}{4{\pi}{{\varepsilon}_0}{r_n^2}}$ центростремительной силе 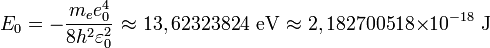$~\frac{m_e v^2}{r}$ получим:

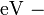
$~{\frac{e_0^2}{4{\pi}{{\varepsilon}_0}{r_n}}}={m_e}{v_n^2}$

Здесь 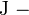$~m_e~-$ масса электрона, 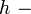$~{v_n}~-$ его скорость на орбите радиуса 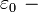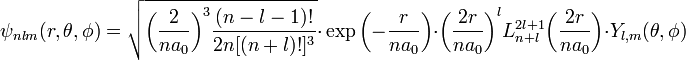$~r_n$ , $~{{\varepsilon}_0}~-$ диэлектрическая проницаемость вакуума.

Отсюда кинетическая энергия электрона

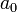
$~{\frac{{m_e}{v_n^2}}{2}}={\frac{e_0^2}{8{\pi}{{\varepsilon}_0}r}}$

где 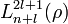$~r~-$ расстояние от электрона до ядра.

Потенциальная его энергия

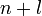
$~{E_{pot}}=-{\frac{e_0^2}{4{\pi}{{\varepsilon}_0}r}}$

Полная энергия, соответственно, равна

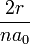
$~E=-{\frac{e_0^2}{8{\pi}{{\varepsilon}_0}r}}$

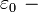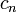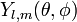Для нахождения радиуса $~r_n$ стационарной орбиты с номером $~n$ рассмотрим систему уравнений, в которой второе есть математическое выражение первого постулата Бора $~{m_e}{v_n}{r_n}={\frac{nh}{2{\pi}}}$ :

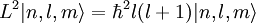
$~\frac{{m_e}{v_n^2}}{r_n}=\frac{e_0^2}{4{\pi}{{\varepsilon}_0}{r_n^2}}$

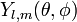
$~{m_e}{v_n}{r_n}={\frac{nh}{2{\pi}}}$

Отсюда получаем выражение для радиуса стационарной орбиты с номером 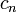$~n$ :

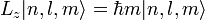
$~{r_n}=\frac{{{\varepsilon}_0}{n^2}{h^2}}{{\pi}{m_e}{e_0^2}}$

Радиус первой орбиты оказывается равным 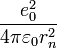$~{r_1}={a_0}~{\approx}~5,291769241{\times}{10^{-11}}$ метра. Эта константа называется боровским радиусом.

Подставляя это значение в выражение для энергии, получим, что

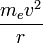
$~{E_n}=-{\frac{1}{n^2}}{\frac{{m_e}{e_0^4}}{8{h^2}{{\varepsilon}_0^2}}}$

Отсюда мы можем найти волновое число фотона, излучаемого атомом водорода за один переход из возбужденного состояния с главным квантовым числом 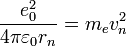$~n_1$ в состояние с неким фиксированным главным квантовым числом $~n_2$ .

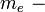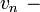
$~{\upsilon}={R_H} \left$

где 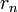$~{R_H}={\frac{{m_e}{e_0^4}}{8{h^3}{{\varepsilon}_0^2}}}~{\approx}~1,097{\times}{10^{5}}~-$ постоянная Ридберга.

<<< Неон

Водород в металлах >>>

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории