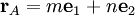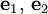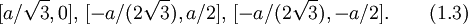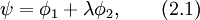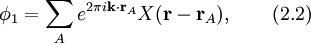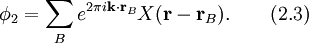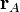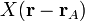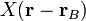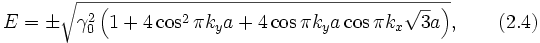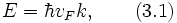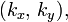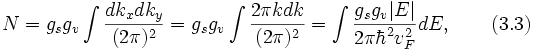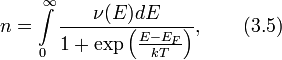Графен - Физика

Химия - Графен - Физика

01 марта 2011

Оглавление:
1. Графен
2. История открытия
3. Получение
4. Дефекты
5. Физика
6. Интересные факты

Физические свойства нового материала можно изучать по аналогии с другими подобными материалами. В настоящее время экспериментальное и теоретическое исследование графена сосредоточено на стандартных свойствах двумерных систем: проводимости, квантовом эффекте Холла, слабой локализации и других эффектах, исследованных ранее в двумерном электронном газе.

Теория

В этом параграфе кратко описываются основные положения теории, некоторые из которых получили экспериментальное подтверждение, а некоторые ещё ждут верификации.

Кристаллическая структура

Рис. 3. Изображение гексагональной решётки графена. Жёлтым цветом показана элементарная ячейка, красным и зелёным цветами показаны узлы различных подрешёток кристалла. e₁ и e₂ — вектора трансляций

Кристаллическая решётка графена представляет собой плоскость, состоящую из шестиугольных ячеек, то есть является двумерной гексагональной кристаллической решёткой. Для такой решётки известно, что её обратная решётка тоже будет гексагональной. В элементарной ячейке кристалла находятся два атома, обозначенные A и B. Каждый из этих атомов при сдвиге на вектора трансляций образует подрешётку из эквивалентных ему атомов, то есть свойства кристалла независимы от точек наблюдения, расположенных в эквивалентных узлах кристалла. На рисунке 3 представлены две подрешётки атомов, закрашенные разными цветами: зелёным и красным.

Расстояние между ближайшими атомами углерода в шестиугольниках, обозначенное a₀, составляет 0,142 нм. Постоянную решётки можно получить из простых геометрических соображений. Она равна $a=\sqrt{3}a_0$ , то есть 0,246 нм. Если определить за начало координат точку, соответствующую узлу кристаллической решётки, из которой начинаются векторы трансляций $\mathbf{e}_1,\,\mathbf{e}_2$ с длиной векторов, равной a, и ввести двумерную декартову систему координат в плоскости графена с осью ординат, направленной вверх, и осью абсцисс, направленной по отрезку, соединяющему соседние узлы A и B, то тогда координаты концов векторов трансляций, начинающихся из начала координат, запишутся в виде:

$\mathbf{e}_1=,\,\mathbf{e}_2=,\qquad$

а соответствующие им вектора обратной решётки:

$\mathbf{g}_1=,\,\mathbf{g}_2=\qquad$

. В декартовых координатах положение ближайших к узлу подрешётки A в начале координат атомов из подрешётки B задаётся в виде:

$,\,,\,.\qquad$

Зонная структура

Кристаллическая структура материала находит отражение во всех его физических свойствах. В особенности сильно от порядка, в котором расположены атомы в кристаллической решётке, зависит зонная структура кристалла.

Рис. 4: Ближайшие атомы в окружении центрального узла решётки. Красная пунктирная окружность соответствует ближайшим соседям из той же самой подрешётки кристалла, а зелёная окружность соответствует атомам из второй подрешётки кристалла

Зонная структура графена рассчитана в статье в приближении сильно связанных электронов. На внешней оболочке атома углерода находится 4 электрона, три из которых образуют связи с соседними атомами в решётке при перекрывании sp²-гибридизированных орбиталей, а оставшийся электрон находится в 2p_z-состоянии. В приближении сильно связанных электронов полная волновая функция всех электронов кристалла записывается в виде суммы волновых функций электронов из разных подрешёток

$\psi=\phi_1+\lambda\phi_2,\qquad$

где коэффициент λ — некий неизвестный параметр, который определяется из минимума энергии. Входящие в уравнение волновые функции φ₁ и φ₂ записываются в виде суммы волновых функций отдельных электронов в различных подрешётках кристалла

$\phi_1=\sum_Ae^{2\pi i\mathbf{k}\cdot \mathbf{r}_A}X,\qquad$

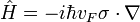$\phi_2=\sum_Be^{2\pi i\mathbf{k}\cdot \mathbf{r}_B}X.\qquad$

Здесь $\mathbf{r}_A$ и $\mathbf{r}_B$ — радиус-векторы, направленные на узлы кристаллической решётки, а 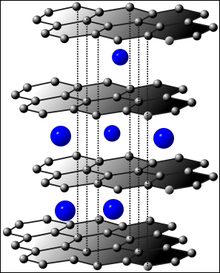$X$ и $X$ — волновые функции электронов, локализованных вблизи этих узлов.

В приближении сильно связанных электронов интеграл перекрытия, то есть сила взаимодействия, быстро спадает на межатомных расстояниях. Другими словами — взаимодействие волновой функции центрального атома с волновыми функциями атомов, расположенных на зелёной окружности, вносит основной вклад в формирование зонной структуры графена.

Энергетический спектр электронов в графене имеет вид)

$E=\pm\sqrt{\gamma_0^2\left},\qquad$

где знак «+» соответствует электронам, а «-» — дыркам.

Линейный закон дисперсии

Рис. 5. Изолинии постоянной энергии). Жирный чёрный шестиугольник — первая зона Бриллюэна. Показаны также красные окружности на краях первой зоны Бриллюэна, где закон дисперсии носителей линеен. K и K' обозначают две долины в k-пространстве с неэквивалентными волновыми векторами

Из уравнения следует, что вблизи точек соприкосновения валентной зоны и зоны проводимости закон дисперсии для носителей в графене представляется в виде:

$E=\hbar v_Fk,\qquad$

где v_F — скорость Ферми, k — модуль волнового вектора в двумерном пространстве с компонентами 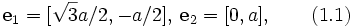$,$ отсчитанного от K или K' точек Дирака, $\hbar$ — постоянная Планка. Здесь следует отметить, что такого рода спектром обладает фотон, поэтому говорят, что квазичастицы в графене обладают нулевой эффективной массой. Скорость Ферми v_F играет роль «эффективной» скорости света. Так как электроны и дырки — фермионы, то они должны описываться уравнением Дирака, но с нулевой массой частиц и античастиц. Кроме того, так как графен — двухдолинный полуметалл, то уравнение Дирака должно быть модифицировано для учёта электронов и дырок из разных долин. В итоге мы получим восемь дифференциальных уравнений первого порядка, которые включают такие характеристики носителей, как принадлежность к определённой подрешётке кристалла, нахождение в долине и проекцию спина. Решения этих уравнений описывают частицы с положительной энергией и античастицы с отрицательной энергией. Обычно спин электрона не принимают во внимание, и гамильтониан уравнения Дирака записывается в виде:

$H_0=-i\hbar v \left( \begin{array}{cc} \mathbf{\sigma}\mathbf{\nabla} & 0 \\ 0 & \mathbf{\sigma^{*}\nabla} \\ \end{array} \right) =-i\hbar v \left( \begin{array}{cccc} 0 & \nabla_x-i\nabla_y & 0 & 0 \\ \nabla_x+i\nabla_y & 0 & 0 & 0 \\ 0 & 0 & 0 & \nabla_x+i\nabla_y \\ 0 & 0 & \nabla_x-i\nabla_y & 0 \\ \end{array} \right),\qquad$

где $\mathbf{\sigma}=$ — вектор-строка, состоящий из матриц Паули.

Линейный закон дисперсии приводит к линейной зависимости плотности состояний от энергии, в отличие от обычных двумерных систем с параболическим законом дисперсии, где плотность состояний не зависит от энергии. Плотность состояний в графене задаётся стандартным способом

$N=g_sg_v\int{\frac{dk_xdk_y}{^2}}=g_sg_v\int{\frac{2\pi kdk}{^2}}=\int{\frac{g_sg_v|E|}{2\pi \hbar^2v_F^2}dE},\qquad$

где выражение под интегралом и есть искомая плотность состояний:

$\nu=\frac{g_sg_v}{2\pi \hbar^2v_F^2}|E|,\qquad$

где g_s и g_v — спиновое и долинное вырождение соответственно, а модуль энергии появляется, чтобы описать электроны и дырки одной формулой. Отсюда видно, что при нулевой энергии плотность состояний равна нулю, то есть отсутствуют носители.

Концентрация электронов задаётся интегралом по энергии

$n=\int\limits_0^{\infty}{\frac{\nudE}{1+\exp{\left}}},\qquad$

где E_F — уровень Ферми. Если температура мала по сравнению с уровнем Ферми, то можно ограничиться случаем вырожденного электронного газа

$n=\int\limits_0^{E_F}{\frac{g_sg_vEdE}{2\pi \hbar^2v_F^2}}=\frac{g_sg_v}{2\pi \hbar^2v_F^2}\frac{E_F^2}{2}.\qquad$

Концентрацией носителей управляют с помощью затворного напряжения. Они связаны простым соотношением 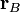$n=7,2\cdot10^{14} V_g$ .

Здесь также следует обратить внимание на тот факт, что появление линейного закона дисперсии при рассмотрении гексагональной решётки не является уникальной особенностью для данного типа кристаллической структуры, а может появляться и при существенном искажении решётки вплоть до квадратной решётки.

Эффективная масса

Благодаря линейному закону дисперсии эффективная масса электронов и дырок в графене равна нулю. Но в магнитном поле возникает другая масса, связанная с движением электрона по замкнутым орбитам и называемая циклотронной массой. Связь между циклотронной массой и энергетическим спектром для носителей в графене получается из следующего рассмотрения. Энергия уровней Ландау для уравнения Дирака задаётся в виде

$E_{LL}=\sqrt{2e\hbar v_F^2B\left},\qquad$

где «±» соответствует спиновому расщеплению. Плотность состояний в графене осциллирует как функция обратного магнитного поля, и её частота равна

$B_F=\frac{\hbar}{2\pi e}S,\qquad$

где S = πk — площадь орбиты в пространстве волновых векторов на уровне Ферми. Осциллирующий характер плотности состояний приводит к осцилляциям магнетосопротивления, что эквивалентно эффекту Шубникова — де Гааза в обычных двумерных системах. Исследуя температурную зависимость амплитуды осцилляций, находят циклотронную массу носителей.

Из периода осцилляций также можно определить концентрацию носителей

$B_F=\frac{h}{4e}n.\qquad$

Циклотронная масса связана с площадью орбиты следующим соотношением

$m_c=\frac{\hbar^2}{2\pi}\frac{\partial S}{\partial E}.\qquad$

Если принять во внимание линейный закон дисперсии для носителей в графене, то зависимость эффективной массы от концентрации задаётся формулой

$m_c=\frac{\hbar k_F}{v_F}=\frac{E}{v_F^2}=\left^{1/2}.\qquad$

Согласие этой корневой зависимости с экспериментальными результатами стало доказательством линейности закона дисперсии в графене.

Хиральность и парадокс Клейна

Рассмотрим часть гамильтониана для долины K):

$H_0^K=-i\hbar v\mathbf{\sigma}\mathbf{\nabla}.\qquad$

Матрицы Паули здесь не имеют отношения к спину электрона, а отражают вклад двух подрешёток в формирование двухкомпонентной волновой функции частицы. Матрицы Паули являются операторами псевдоспина по аналогии со спином электрона. Данный гамильтониан полностью эквивалентен гамильтониану для нейтрино, и, как и для нейтрино, существует сохраняющаяся величина проекции спина на направление движения — величина, называемая спиральностью. Для электронов хиральность положительна, а для дырок — отрицательна. Сохранение хиральности в графене приводит к такому явлению, как парадокс Клейна. В квантовой механике с этим явлением связано нетривиальное поведение коэффициента прохождения релятивистской частицей потенциальных барьеров, высота которых больше, чем удвоенная энергия покоя частицы. Частица более легко преодолевает более высокий барьер. Для частиц в графене можно построить аналог парадокса Клейна с той разницей, что не существует массы покоя. Можно показать, что электрон преодолевает с вероятностью, равной единице, любые потенциальные барьеры при нормальном падении на границу раздела. Если падение происходит под углом, то существует некоторая вероятность отражения. Например, обычный p-n переход в графене является таким преодолимым барьером. В целом парадокс Клейна приводит к тому, что частицы в графене трудно локализовать, что в свою очередь приводит, например, к высокой подвижности носителей в графене. Недавно были предложены несколько моделей, позволяющих локализовать электроны в графене. В работе впервые продемонстрирована квантовая точка из графена и измерена кулоновская блокада при 0,3 К.

Эффект Казимира

Эффект Казимира определяет взаимодействие любых электрически нейтральных объектов на малых расстояниях. В случае реалистичных материалов величина взаимодействия обуславливается объёмными свойствами материала. Однако расчёты показывают, что и для моноатомных слоёв графена сила Казимира может быть сравнительно велика, а наблюдение эффекта может быть доступно экспериментально.

Эксперимент

Подавляющее большинство экспериментальных работ посвящено графену, полученному отшелушиванием объёмного кристалла пиролитического графита.

Проводимость

Теоретически показано, что основное ограничение на подвижность электронов и дырок в графене возникает из-за заряженных примесей в диэлектрике, поэтому сейчас ведутся работы по получению свободновисящих плёнок графена, что должно увеличить подвижность до 2×10 см²·В·c. В настоящее время максимальная достигнутая подвижность составляет 2×10 см²·В·c; она была получена в образце, подвешенном над слоем диэлектрика на высоте 150 нм. Образец с толщиной в один атом поддерживался при помощи широких контактов. Для улучшения подвижности образец подвергался очистке от примесей на поверхности посредством пропускания тока, который нагревал весь образец до 900 К в высоком вакууме.

Идеальную двумерную плёнку в свободном состоянии нельзя получить из-за её термодинамической нестабильности. Но если в плёнке будут дефекты или она будет деформирована в пространстве, то такая «неидеальная» плёнка может существовать без контакта с подложкой. В эксперименте с использованием просвечивающего электронного микроскопа было показано, что свободные плёнки графена существуют и образуют поверхность сложной волнистой формы, с латеральными размерами пространственных неоднородностей около 5—10 нм и высотой 1 нм. В статье было показано, что можно создать свободную от контакта с подложкой плёнку, закреплённую с двух краёв, образуя, таким образом, наноэлектромеханическую систему. В данном случае подвешенный графен можно рассматривать как мембрану, изменение частоты механических колебаний которой предлагается использовать для детектирования массы, силы и заряда, то есть использовать в качестве высокочувствительного сенсора.

Подложка кремния с диэлектриком, на котором покоится графен, должна быть сильно легирована, чтобы её можно было использовать в качестве обратного затвора, при помощи которого можно управлять концентрацией и даже изменять тип проводимости. Поскольку графен является полуметаллом, то приложение положительного напряжения к затвору приводит к электронной проводимости графена, и напротив — если приложить отрицательное напряжение, то основными носителями станут дырки, поэтому в принципе нельзя обеднить полностью графен от носителей. Заметим, что если графит состоит из нескольких десятков слоёв, то электрическое поле достаточно хорошо экранировано, как и в металлах, огромным количеством носителей в полуметалле.

В идеальном случае, когда отсутствует легирование и затворное напряжение равно нулю, не должно быть носителей тока, что, если следовать наивным представлениям, должно приводить к отсутствию проводимости. Но, как показывают эксперименты и теоретические работы, вблизи дираковской точки или точки электронейтральности для дираковских фермионов существует конечное значение проводимости, хотя величина минимальной проводимости зависит от метода расчёта. Эта идеальная область не изучена просто потому, что нет достаточно чистых образцов. В действительности все плёнки графена соединены с подложкой, и это приводит к неоднородностям, флуктуациям потенциала, что ведёт к пространственной неоднородности типа проводимости по образцу, поэтому даже в точке электронейтральности концентрация носителей теоретически не меньше, чем 10 см. Здесь проявляется отличие от обычных систем с двумерным электронным или дырочным газом, а именно — отсутствует переход металл-диэлектрик.

Квантовый эффект Холла

Впервые необычный квантовый эффект Холла наблюдали в работах, где было показано, что носители в графене действительно обладают нулевой эффективной массой, поскольку положения плато на зависимости недиагональной компоненты тензора проводимости соответствовали полуцелым значениям холловской проводимости 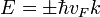$\nu=\pm$ в единицах 4e / h, то есть 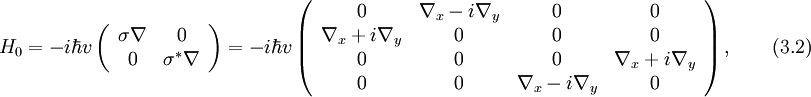$\sigma_{xy}=\pm4e^2/h.$ Это квантование согласуется с теорией квантового эффекта Холла для дираковских безмассовых фермионов. Сравнение целочисленного квантового эффекта Холла в обычной двумерной системе и графене см. на рисунке 6. Здесь показаны уширенные уровни Ландау для электронов и для дырок. Если уровень Ферми находится между уровнями Ландау, то на зависимости холловской проводимости σ_xy наблюдается ряд плато. Эта зависимость отличается от обычных двумерных систем.

Квантовый эффект Холла может использоваться как эталон сопротивления, потому что численное значение наблюдаемого в графене плато, равное h / 2e, воспроизводится с хорошей точностью, хотя качество образцов уступает высокоподвижному ДЭГ в GaAs и, соответственно, точности квантования. Преимущество КЭХ в графене в том, что он наблюдается при комнатной температуре. Основное ограничение на наблюдение КЭХ при комнатной температуре накладывает не само размытие распределения Ферми-Дирака, а рассеяние носителей на примесях, что приводит к уширению уровней Ландау.

Рис. 6. a) Квантовый эффект Холла в обычной двумерной системе. b) Квантовый эффект Холла в графене. g = g_sg_v = 4 — вырождение спектра

В современных образцах графена вплоть до 45 Т невозможно наблюдать дробный квантовый эффект Холла, но наблюдается целочисленный квантовый эффект Холла, который не совпадает с обычным. В работе наблюдается спиновое расщепление релятивистских уровней Ландау и снятие четырёхкратного вырождения для наинизшего уровня Ландау вблизи точки электронейтральности. Для объяснения этого эффекта предложено несколько теорий, но недостаточное количество экспериментального материала не позволяет выбрать среди них правильную.

Благодаря отсутствию запрещённой зоны в графене в структурах с верхним затвором можно сформировать непрерывный p-n переход, когда напряжение на верхнем затворе позволяет инвертировать знак носителей, задаваемый обратным затвором в графене, где концентрация носителей никогда не обращается в ноль. В таких структурах тоже можно наблюдать квантовый эффект Холла, но из-за неоднородности знака носителей значения холловских плато отличаются от приведённых выше. Для структуры с одним p-n переходом значения квантования холловской проводимости описываются формулой

$G=\frac{2e^2}{h}\frac{|\nu^{'}||\nu|}{|\nu^{'}|+|\nu|},\qquad$

где ν и ν — факторы заполнения в n- и p-области соответственно, которые могут принимать значения 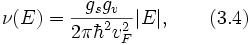$\pm2, \pm6, \pm10$ и т. д. Тогда плато в структурах с одним p-n переходом наблюдаются при значениях 1, 3/2, 2, и т. д.

Для структуры с двумя p-n переходами соответствующие значения холловской проводимости равны

$G=\frac{e^2}{h}\frac{|\nu^{'}||\nu|}{2|\nu^{'}|+|\nu|}=\frac{2}{3},\frac{6}{5},\frac{6}{7},....\qquad$

<<< ДНК-машина

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории