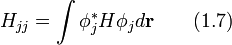Химия - Квантовый эффект Холла в графене

01 марта 2011


Оглавление:
1. Квантовый эффект Холла в графене
2. Квантовый эффект Холла



Квантовый эффект Холла в графене или необычный квантовый эффект Холла — эффект квантования холловского сопротивления или проводимости двумерного электронного газа или двумерного дырочного газа в сильных магнитных полях в графене. Этот эффект был предсказан теоретически и подтверждён экспериментально в 2005 году.

Уровни Ландау

См. также «Физический портал»

Уровни Ландау в графене описываются уравнением Дирака для графена с учётом магнитного поля, которое можно записать в виде

\psi=\varepsilon\psi

где использована калибровка Ландау для векторного потенциала 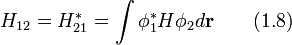\vec{A}=, двумерный градиент равен 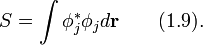\vec{\nabla}=, а вектор 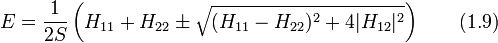\vec{\sigma} составлен из матриц Паули . В матричном виде уравнение запишется в виде

\begin{pmatrix} 0 & -i\hbar v\frac{\partial}{\partial x}-\hbar v\frac{\partial}{\partial y}+eBy\\ -i\hbar v_F\frac{\partial}{\partial x}+\hbar v\frac{\partial}{\partial y}+eBy & 0 \end{pmatrix}\psi=\varepsilon\psi.

Здесь можно легко разделить переменные и в итоге прийти к спектру для релятивистских уровней Ландау

\varepsilon_n=\pm\hbar\tilde{\omega_c}\sqrt{n}=\pm\sqrt{\hbar v_F^2eB2n/c},

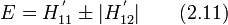где n=0,\,1,\,2,... , «циклотронная частота» равна 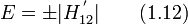\tilde{\omega_c}=\sqrt{2}\frac{v_F}{l_B}, магнитная длина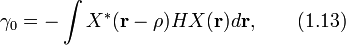 l_B=\sqrt{\frac{\hbar c}{eB}}.



Просмотров: 2410


<<< Зонная структура графена
Осцилляции Шубникова де Гааза (графен) >>>


Химики   
Бытовая химия   
Химические вещества   
Химические законы и уравнения   
История химии   
Лабораторная техника   
Химическое машиностроение   
Награды в области химических наук   
Химическая номенклатура   
Химическое образование   
Химические общества   
Химическая промышленность   
Разделы химии   
Химические реакции   
Химические свойства   
Химическая связь   
Химические системы   
Химические теории