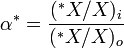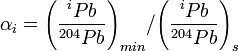Механизм реакции Белоусова Жаботинского

Химия - Механизм реакции Белоусова Жаботинского

01 марта 2011

Оглавление:
1. Механизм реакции Белоусова Жаботинского
2. Расширенный Орегонатор

Модель Жаботинского — Корзухина

Первая модель реакции Белоусова — Жаботинского была получена в 1967 году Жаботинским и Корзухиным на основе подбора эмпирических соотношений, правильно описывающих колебания в системе. В её основе лежала знаменитая консервативная модель Лотки — Вольтерра.

$\frac{d X_1}{dt} = k_1 X_1 - k_0 X_1 X_3$

$\frac{d X_2}{dt} = k_1 X_1 - k_2 X_2$

$\frac{d X_3}{dt} = k_2 X_2 - k_3 X_4$

здесь X₂ =, C=₀ +₀, X₁ — концентрация автокатализатора, X₃ =.

Брюсселятор

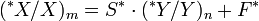
Колебательная динамика модели Брюсселятор и моделирование с её помощью волн

Простейшая модель, предложенная Пригожиным, которая имеет колебательную динамику.

I	A	→	X
II	B + X	→	Y + D
III	2X + Y	→	3X
IV	X	→	E

V	A + B	→	E + D

Орегонатор

Механизм, предложенный Филдом и Нойесом, является одним из простейших и в то же время наиболее популярным в работах, исследующих поведение реакции Белоусова-Жаботинского:

I	A + Y	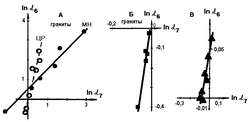$\longrightarrow$	X
II	X + Y	$\longrightarrow$	P
III	B + X	$\longrightarrow$	2 X + Z
IV	2 X	$\longrightarrow$	Q
V	Z	$\longrightarrow$	f Y

Соответствующая система обыкновенных дифференциальных уравнений:

$\frac{d}{dt}= k_I - k_{II} + k_{III} - k_{IV}^2$

$\frac{d}{dt}= -k_I - k_{II} + f k_V$

$\frac{d}{dt}= k_{III} - k_V$

Эта модель демонстрирует простейшие колебания, похожие на экспериментально наблюдаемые, однако она не способна показывать более сложные типы колебаний, например сложнопериодические и хаотические.

<<< Реакция Белоусова Жаботинского

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории