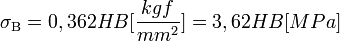Химия - Модуль упругости
01 марта 2011общее название нескольких физических величин, характеризующих способность твёрдого тела упруго деформироваться при приложении к ним силы. В области упругой деформации модуль упругости тела определяется производной зависимости напряжения от деформации, то есть тангенсом угла наклона диаграммы напряжений-деформаций):
где λ — модуль упругости; p — напряжение, вызываемое в образце действующей силой; 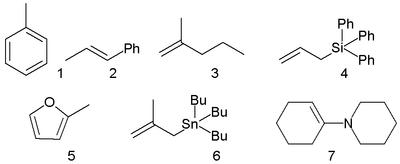 — упругая деформация образца, вызванная напряжением. Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения λ также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
— упругая деформация образца, вызванная напряжением. Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения λ также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:
- Модуль Юнга характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к удлинению. Часто модуль Юнга называют просто модулем упругости.
- Модуль сдвига или модуль жесткости характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения). Модуль сдвига является одной из составляющих явления вязкости.
- Модуль объёмной упругости или Модуль объёмного сжатия характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения, одинакового по всем направлениям. Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля.
Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.
Гомогенные и изотропные материалы, обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.
В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.
| Формулы преобразования | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Упругие свойства гомогенных изотропных линейно-упругих материалов уникально определяются любыми двумя модулями упругости. Таким образом, имея два модуля, остальные можно вычислить по следующим формулам: | |||||||||
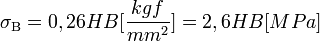 |
 |
 |
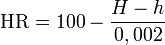 |
 |
 |
 |
 |
 |
|
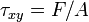 |
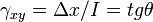 |
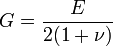 |
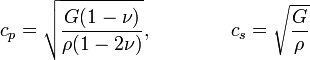 |
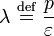 |
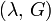 |
||||
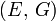 |
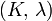 |
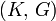 |
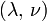 |
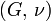 |
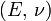 |
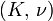 |
|||
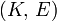 |
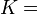 |
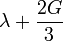 |
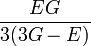 |
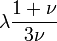 |
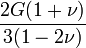 |
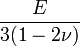 |
|||
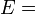 |
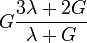 |
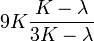 |
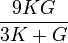 |
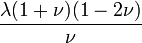 |
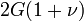 |
||||
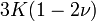 |
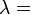 |
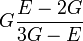 |
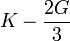 |
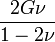 |
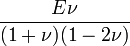 |
||||
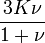 |
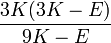 |
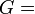 |
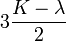 |
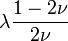 |
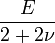 |
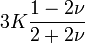 |
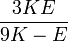 |
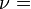 |
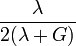 |
Модули упругости для некоторых веществ:
| Материал | Е, МПа | Е, кгс/см² |
|---|---|---|
| Алюминий | 70000 | 713 800 |
| Вода | 2030 | 20300 |
| Дерево | 10000 | 102 000 |
| Кость | 30000 | 305 900 |
| Медь | 100000 | 1 020 000 |
| Резина* | 10 | 102 |
| Сталь | 200000 | 2 039 000 |
| Стекло | 70000 | 713 800 |
Просмотров: 4022
|
|