Молекула водорода - Движение ядер в молекуле водорода

Химия - Молекула водорода - Движение ядер в молекуле водорода

01 марта 2011

Оглавление:
1. Молекула водорода
2. Волновые функции
3. Энергия электронных состояний
4. Зависимость энергии основного состояния от расстояния между ядрами
5. Движение ядер в молекуле водорода
6. Пара- и ортоводород

Гамильтониан, описывающий относительное движение двух ядер в молекуле водорода имеет вид

$\hat{H}_{nucl} = - \frac{\hbar^2}{2\mu R^2} \frac{\partial }{\partial R} \left + \frac{\hat{L}^2}{2\mu R^2} + \mathcal{E}_{sym}$ ,

где μ = M / 2 — приведённая масса двух ядер, 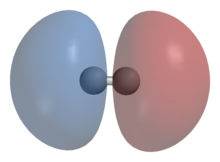$\mathcal{E}_{sym}$ — энергия синглетного электронного состояния, зависящая от расстояния между ядрами, 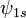$\hat{L}$ — оператор углового момента, описывающий вращение молекулы.

Вращение

Оператор углового момента коммутирует с гамильтонианом, поэтому собственные функции гамильтониана можно выбрать общими с собственными функциями оператора углового момента, то есть сферические гармоники:

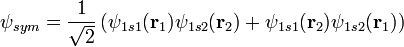$\hat{L}^2 Y_{lm} = \hbar^2 l Y_{lm}$ .

Вклад вращения в энергию молекулы равен

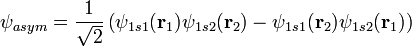$E_{rot} = \frac{\hbar^2 l}{2\mu R^2}$ .

Этот вклад мал, потому, что массы ядер намного больше, чем массы электронов. Он зависит от расстояния между ядрами R. При колебаниях ядер это расстояние меняется, поэтому вращательное движение, строго говоря, невозможно отделить от колебательного. Однако при малых l и при малых энергиях колебательного движения можно считать, что R равняется определённому среднему значению.

Вращательные уровни вырождены относительно магнитного квантового числа m_l. Кратность выроджения 2l+1.

Колебания атомов

Вблизи минимума функцию 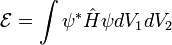$\mathcal{E}_{sym} + \frac{\hbar^2 l}{2\mu R^2}$ можно разложить в ряд Тейлора, ограничившись только квадратичным членом.

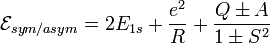$U \approx \mathcal{E}_{sym} + \frac{\hbar^2 l}{2\mu R^2} = \mathcal{E} + \frac{\hbar^2 l}{2\mu R^2_0} + \frac {\mu \omega^2}{2}$ ,

где

$\mu\omega^2 = \left. \frac{d^2U}{dR^2} \right|_{R=R_0}$

Таким образом, задача об энергетических состояниях колебания ядер сводится к задаче квантового гармонического осциллятора. Следовательно, для низших колебательных и вращательных уровней энергия молекулы водорода равна

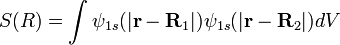$E_{s,n,l} = \mathcal{E}_{sym} + \frac{\hbar^2 l}{2\mu R^2} + \hbar \omega \left$ ,

где 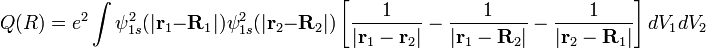$v = 0, 1 \ldots$ — колебательное квантовое число.

Низшая энергия колебания 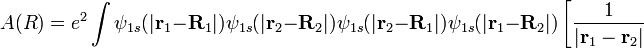$\frac{\hbar \omega}{2}$ отвечает нулевым колебаниям.

При больших значениях квантовых чисел n и l колебательное и вращательное движение разделить невозможно.

Таким образом, энергию молекулы при малых квантовых числах можно записать в виде трёх слагаемых — электронного, колебательного и вращательного:

E_s,n,l = E_el + E_v + E_r

Малым параметром задачи является отношение массы электрона к массе протона. Электронное слагаемое не зависит от этого отношения, колебательное пропорционально 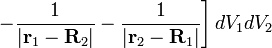$\sqrt{m/M}$ , вращательное пропорционально m / M. Поэтому

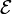$E_{el} \gg E_v \gg E_r$ .

Следовательно, электронный уровень расщепляется на несколько колебательных, каждый из которых, в свою очередь, расщепляется на вращательные. Поскольку энергии вращательных уровней близки, то в оптических спектрах они сливаются в полосы — образуется полосатый спектр, который наблюдается для молекулы HD. Для симметричной молекулы H₂ переходы между орбитальными и колебательными уровнями запрещены правилами отбора, поэтому молекулярный протий не поглощает в инфракрасной области.

<<< Макромолекула

Раскраска по CPK >>>

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории