Химия - Нуклеофил - Шкалы нуклеофильности
01 марта 2011Оглавление:
1. Нуклеофил
2. Примеры
3. Шкалы нуклеофильности
Известно несколько способов количественного описания реакционной способности нуклеофилов. Приведенные ниже методы основаны на изучении экспериментальных данных о скорости определенных реакций с участием большого количества нуклеофилов и электрофилов. Как правило, реагенты с выраженным альфа-эффектом не включаются в эти корреляции.
Уравнение Свена-Скотта
Уравнение Свена-Скотта было выведено в 1953 году и является первой попыткой количественно описать реакционную способность нуклеофилов в реакциях SN2:
В этом уравнении k — константа скорости реакции стандартного субстрата с данным нуклеофилом, k0 — константа скорости реакции субстрата со стандартным нуклеофилом, S — параметр чувствительности субстрата к изменению нуклеофила, n — параметр нуклеофильности.
Таким образом, для реакций
- CH3I + H2O → CH3OH + HI
- CH3I + Nuc−H → CH3−Nuc + HI
уравнение Свена-Скотта можно записать как
| Нуклеофил | Значение n | Нуклеофил | Значение n | Нуклеофил | Значение n |
|---|---|---|---|---|---|
| SO3 | 5,16 | CN | 5,10 | I | 5,04 |
| SCN | 4,77 | HO | 4,20 | N3 | 4,00 |
| Br | 3,89 | HCO3 | 3,80 | Cl | 3,04 |
| CH3COO | 2,72 | SO4 | 2,50 | F | 2,00 |
| NO3 | 1,03 | CH3OH | 0,70 | H2O | 0,00 |
| Нуклеофил | Значение n | Нуклеофил | Значение n | Нуклеофил | Значение n |
|---|---|---|---|---|---|
| F | 2,7 | Cl | 4,37 | Br | 5,79 |
| I | 7,42 | N3 | 5,78 | NC | 6,70 |
| CH3OH | ~0,00 | H2O | 0,00 | CH3CO2 | 4,3 |
| PhO | 5,75 | CH3O | 6,29 | Пиридин | 5,23 |
| Анилин | 5,70 | Триэтиламин | 6,66 | PhSH | 5,7 |
Уравнение Ричи
Уравнение Ричи было выведено в 1972 году и выражается следующим образом:
-
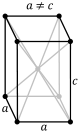 ,
,
где k0 — константа скорости реакции стандартного катиона с со стандартным нуклеофилом в водной среде, k — константа скорости реакции с заданным нуклеофилом, N — параметр, зависящий от нуклеофила:
| Нуклеофил |
Значение N | Нуклеофил |
Значение N |
|---|---|---|---|
| H2O | 0,0 | MeOH | 0,5 |
| CN | 3,8 | CN | 5,9 |
| HO | 4,5 | MeO | 7,5 |
| N3 | 5,4 | N3 | 8,5 |
| PhS | 13,1 | PhS | 10,7 |
Важной особенностью уравнения Ричи является отсутствие параметра чувствительности субстрата. Таким образом, принимается, что относительная реакционная способность двух нуклеофилов определяется только значением N и не зависит от партнера по реакции. Это находится в резком противоречии с т. н. принципом взаимозависимости реакционной способности и селективности. Из-за этого уравнение Ричи иногда называется «соотношение постоянной селективности». Явная упрощенность вызвала ряд публикаций о пределах его применимости.
Уравнение Майра-Патца
В 1994 г. Г. Майр и М. Патц, на основании исследования реакционной способности диарилметильных катионов и других соединений, предложили уравнение, описывающее реакционную способность достаточно большого количества нуклеофилов и электрофилов :
В этом уравнении константа скорости реакции второго порядка k, измеренная при 20 °C, связывается с параметром электрофильности Eметильного катиона E = 0), параметром нуклеофильности N и фактором чувствительности s. Для реакций незаряженных нуклеофилов константа скорости слабо зависит от растворителя и последний обычно не указывается.
Диарилметильные катионы были выбраны в качестве стандартных электрофилов потому, что их активностью можно управлять подбором заместителя R в пара-положении. Таким образом, оказалось возможным измерить реакционную способность очень разных нуклеофилов. Для протестированных соединений параметр N изменяется в диапазоне от −4,47 до 28,95.

| Нуклеофил | N | Нуклеофил | N |
|---|---|---|---|
| 1 | −4,47 | 2 | −0,41 |
| 3 | +0,96 | 4 | −0,13 |
| 5 | +3,61 | 6 | +7,48 |
| 7 | +13,36 | PhCCH3 | 28,95 |
Параметр элекрофильности E для некоторых карбокатионов можно грубо оценить по следующему уравнению :
 ,
,
где kw — константа псевдопервого порядка для реакции карбокатиона с водой при 20 °C.
Нуклеофильность N в уравнении Майра-Патца связана с параметром Ричи N+ следующим соотношением:
Объединенное уравнение
В попытке объединить все вышеописанные уравнения Майр с сотрудниками предложили следующее выражение:
 ,
,
где sE — параметр чувствительности электрофила; sN — параметр чувствительности электрофила; N и E имеют такое же значение, как и в уравнении Майра-Патца.
С помощью соответствующих подстановок данное выражение можно превратить в любое описанное ранее уравнение:
- при sE = 1 это уравнение эквивалентно оригинальному уравнению Майра-Патца;
- при sN = 0.6:
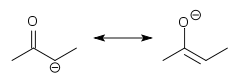 ,
,- что эквивалентно уравнению Свена-Скотта:
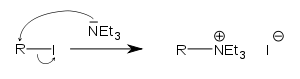 ;
;
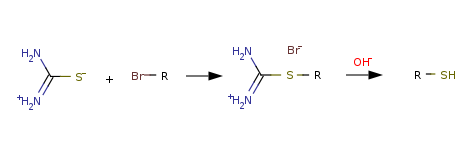
- при sE = 1 и sN = 0.6 получим:

- что эквивалентно уравнению Ричи в немного измененном виде:
Просмотров: 7494
|
|