Химия - Пар-жидкость-кристалл - Механизм роста

Формирование капель катализатора

Figure 4: Schematic illustration of metal-alloy catalyzed whisker growth depicting the catalyst droplet formation during the early stages of whisker growth.

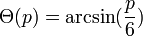
The materials system used, as well as the cleanliness of the vacuum system and therefore the amount of contamination and/or the presence of oxide layers at the droplet and wafer surface during the experiment, both greatly influence the absolute magnitude of the forces present at the droplet/surface interface and, in turn, determine the shape of the droplets. The shape of the droplet, i.e. the contact angle can, be modeled mathematically, however, the actual forces present during growth are extremely difficult to measure experimentally. Nevertheless, the shape of a catalyst particle at the surface of a crystalline substrate is determined by a balance of the forces of surface tension and the liquid-solid interface tension. The radius of the droplet varies with the contact angle as:

where r₀ is the radius of the contact area and β₀ is defined by a modified Young’s equation:

,

It is dependent on the surface and liquid-solid interface tensions, as well as an additional line tension which comes into effect when the initial radius of the droplet is small. As a nanowire begins to grow, its height increases by an amount dh and the radius of the contact area decreases by an amount dr. As the growth continues, the inclination angle at the base of the nanowires increases, as does β₀:

.

The line tension therefore greatly influences the catalyst contact area. The most import result from this conclusion is that different line tensions will result in different growth modes. If the line tensions are too large, nanohillock growth will result and thus stop the growth.

Диаметр нановискеров

The diameter of the nanowire which is grown depends upon the properties of the alloy droplet. The growth of nano-sized wires requires nano-size droplets to be prepared on the substrate. In an equilibrium situation this is not possible as the minimum radius of a metal droplet is given by

where V_l is the molar volume of the droplet, σ_lv the liquid-vapor surface energy, and s is the degree of supersaturation of the vapor. This equations restricts the minimum diameter of the droplet, and of any crystals which can be grown from it, under typically conditions to well above the nanometer level. Several techniques to generate smaller droplets have been developed, including the use of monodispersed nanoparticles spread in low dilution on the substrate, and the laser ablation of a substrate-catalyst mixture so to form a plasma which allows well-separated nanoclusters of the catalyst to form as the systems cools.

Кинетика роста вискеров

During VLS whisker growth, the rate at which whiskers grow is dependent on the whisker diameter: the larger the whisker diameter, the faster the nanowire grows axially. This is due to the fact that the supersaturation of the metal-alloy catalyst is the main driving force for nanowhisker growth and decreases with decreasing whisker diameter:

.

Again, Δµ is the main driving force for nanowhisker growth. More specifically, Δµ₀ is the difference between the chemical potential of the depositing species in the vapor and solid whisker phase. Δµ is the initial difference proceeding whisker growth, while Ω is the atomic volume of Si and α the specific free energy of the wire surface. Examination of the above equation, indeed reveals that small diameters exhibit small driving forces for whisker growth while large wire diameters exhibit large driving forces.