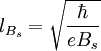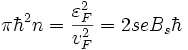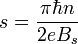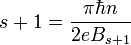Химия - Парадокс Клейна (графен) - Теория

Коэффициент прохождения через симметричный прямоугольный барьер, при изменении ширины барьера от 25 нм до 150 нм в полярных координатах.

Квазичастицы в графене описываются двумерным гамильтонианом для безмассовых дираковских частиц

где — постоянная Планка, v_F — Ферми скорость, σ = — вектор оставленный из матриц Паули, 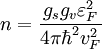— оператор набла. Пусть есть потенциальный барьер с высотой V₀ и шириной D, а энергия налетающих частиц равна E. Тогда из решения уравнения Дирака для областей слева барьера, в самом барьере и справа от барьера запишутся в виде плоских волн как для свободных частиц:

где приняты следующие обозначения для углов φ = arctan, θ = arctan, и волновых векторов в I-ой и III-ей областях k_x = k_Fcosφ, k_y = k_Fsinφ, и во II-ой области под барьером 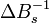, знаков следующих выражений s = sign и s' = sign. Неизвестные коэффициенты r, t амплитуды отражённой и прошедшей волны соответственно находятся из непрерывности волновой функции на границах потенциала.

Для коэффициента прохождения как функции угла падения частицы получено следующее выражение

На рисунке справа показано как изменяется коэффициент прохождения в зависимости от ширины барьера. Показано, что максимальная прозрачность барьера наблюдается при нулевом угле всегда, а при некоторых углах возможны резонансы.