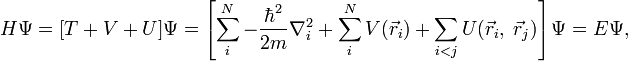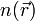Теория функционала плотности - Формальное обоснование метода

Химия - Теория функционала плотности - Формальное обоснование метода

01 марта 2011

Оглавление:
1. Теория функционала плотности
2. Описание метода
3. Формальное обоснование метода
4. Приближения
5. Обобщение на случай магнитного поля
6. Применения
7. Программное обеспечение, которое реализует метод теории функционала плотности

Согласно приближению Борна — Оппенгеймера, которое применяется в большинстве расчётов электронной структуры, ядра, входящие в состав рассматриваемой системы, считаются неподвижными. Электростатический потенциал V, создаваемый этими «неподвижными» ядрами, является внешним для электронов. Стационарное состояние электронов описывается волновой функцией 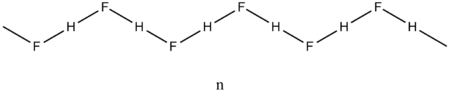$\Psi$ , которая является решением уравнения Шрёдингера

$H\Psi=\Psi=\left\Psi=E\Psi,$

где H — гамильтониан электронной подсистемы, N — количество электронов, U описывает электрон-электронное взаимодействие. Операторы T и U одинаковы для всех систем, в то время как вид V зависит от конкретной системы. Как видно, основное отличие одночастичной задачи от задачи многих тел состоит в наличии слагаемого, описывающего электрон-электронное взаимодействие, U. Существует большое количество методов решения многочастичного уравнения Шрёдингера, основанных на разложении волновой функции с использованием определителя Слэтера. Простейший из них — метод Хартри — Фока, на основе которого развит ряд современных методов. Общей проблемой для них является значительная вычислительная трудоёмкость, из-за которой область применения метода Хартри — Фока и производных от него ограничена не слишком большими системами.

Метод теории функционала плотности в значительной степени решает проблему расчёта систем, включающих большое число частиц, путём сведения задачи о системе многих тел с потенциалом электрон-электронного взаимодействия U к одночастичной задаче, в которой слагаемое U отсутствует.

Плотность частиц, $n$ , с помощью которой и строится формализм теории функционала плотности, задается выражением:

$n=N\int d^3r_2\int d^3r_3\ldots\int d^3r_N\Psi^*\Psi.$

Хоэнберг и Кон в 1964 показали, что это выражение может быть обращено: по заданной плотности частиц в основном состоянии, $n_0$ , можно найти соответствующую волновую функцию основного состояния $\Psi_0$ . Иными словами, Ψ₀ — единственный функционал от n₀, то есть

Ψ₀ = Ψ₀,

а, следовательно, все остальные наблюдаемые физические величины O также являются функционалами n₀:

$\langle O\rangle=\langle\Psi_0\mid O\mid\Psi_0\rangle.$

В частности, для энергии основного состояния можно записать

$E_0=E=\langle\Psi_0\mid T+V+U\mid\Psi_0\rangle,$

где вклад внешнего потенциала 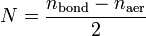$\langle\Psi_0\mid V\mid\Psi_0\rangle$ может быть переписан через плотность частиц:

$V=\int Vn\,d^3r.$

Функционалы T и U одинаковы для всех систем, а V, очевидно, зависит от вида рассматриваемой системы. Для заданной системы вид V известен, и можно минимизировать функционал

$E=T+U+\int Vn\,d^3r$

относительно распределения плотности частиц $n$ , если, конечно, имеются выражения для T и U. В результате минимизации получается плотность частиц в основном состоянии n₀, а вместе с ней и все наблюдаемые в основном состоянии величины.

Вариационная задача отыскания минимума функционала энергии E может быть решена с помощью метода множителей Лагранжа, как это и было сделано Коном и Шэмом в 1965 г. Таким образом, функционал энергии в приведённом выше выражении может быть записан как эффективный функционал плотности частиц в одночастичной системе:

$E_s=\langle\Psi_s\mid T_s+V_s\mid\Psi_s\rangle,$

где T_s означает кинетическую энергию свободной частицы, а V_s — эффективный внешний потенциал для электронной подсистемы. Ясно, что $n_s\,\stackrel{\mathrm{def}}{=}\,n$ если V_s взят в виде

V_s = V + U +.

Решение так называемых уравнений Кона — Шэма для вспомогательной системы, из которой исключено электрон-электронное взаимодействие,

$\left\varphi_i=\varepsilon_i\varphi_i,$

даёт орбитали 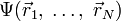$\varphi_i$ , по которым восстанавливается электронная плотность $n$ исходной многочастичной системы:

$n\,\stackrel{\mathrm{def}}{=}\,n_s=\sum_i^N|\varphi_i|^2.$

Эффективный одночастичный потенциал V_s записывается как

$V_s=V+\int\frac{e^2n_s}{|\vec r-\vec r\,'|}\,d^3r'+V_\mathrm{XC},$

где второе слагаемое — слагаемое Хартри — описывает электрон-электронное кулоновское отталкивание, а последнее слагаемое V_XC называется обменно-корреляционным потенциалом. Здесь V_XC включает все многочастичные взаимодействия.

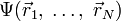Поскольку слагаемое Хартри и член V_XC зависят от плотности $n$ , которая зависит от $\varphi_i$ , которая, в свою очередь, зависит от V_s, решение самосогласованных уравнений Кона — Шэма может быть произведено с помощью итеративной процедуры последовательных приближений. 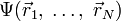Как правило, отталкиваясь от начального приближения для $n$ , рассчитывается соответствующее слагаемое V_s, для которого затем решаются уравнения Кона — Шэма, из которых получается $\varphi_i$ . Отсюда можно получить следующее приближение для плотности и т. д.

<<< Теория молекулярных орбиталей

Химическая технология >>>

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории