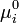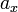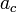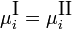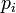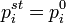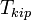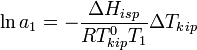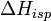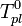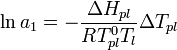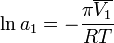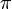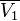Активность (химия) - Методы определения активности

Химия - Активность (химия) - Методы определения активности

06 мая 2011

Оглавление:
1. Активность (химия)
2. Выбор стандартного состояния
3. Методы определения активности

Экспериментальные методы определения активности компонентов в растворе основаны на изучении какого-либо гетерогенного равновесия в системе. При рассмотрении этих методов следует помнить, что в условиях равновесия химические потенциалы i-го компонента в разных фазах равны:

$~\mu_i^\mbox{I}=\mu_i^\mbox{II}$

Это соотношение является исходной точкой для вывода расчетных уравнений в некоторых из методов определения активности. Кроме того, активности компонентов в некоторой фазе связаны между собой уравнением:

$~\sum_{i} x_i d\ln a_i = 0$

По равновесному давлению пара

В основе этого метода лежит соотношение:

$~a_i=\frac{p_i}{p_i^{st}}$

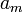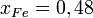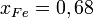где $~p_i$ — парциальное давление пара компонента над раствором, а $~p_i^{st}$ — давление пара этого компонента для стандартного состояния. Соответственно, если за стандартное состояние принято состояние чистого компонента, то $~p_i^{st}=p_i^0$ .

Эксериментальные методы определения давления пара компонентов над раствором весьма разнообразны; выбор того или иного из них определяется, в частности, исследуемой системой.

По повышению температуры кипения раствора

Температура кипения раствора 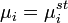$~T_{kip}$ выше температуры кипения чистого растворителя 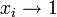$~T_{kip}^0$ . Данные об изменении температуры кипения раствора могут быть использованы для расчета активности растворителя, в соответствии с уравнением:

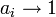$~\ln a_1 = - \frac{\Delta H_{isp}}{RT_{kip}^0T_1}\Delta T_{kip}$ ,

где 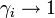$~\Delta H_{isp}$ — теплота испарения растворителя, в интервале от температуры кипения чистого растворителя до температуры кипения раствора принимаемая постоянной. Индексом «1» обычно обозначается растворитель.

По понижению температуры замерзания раствора

Температура замерзания раствора 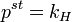$~T_{pl}$ ниже температуры замерзания чистого растворителя 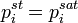$~T_{pl}^0$ . Соответственно, активность растворителя можно рассчитать, используя зависимость:

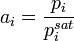$~\ln a_1 = - \frac{\Delta H_{pl}}{RT_{pl}^0T_{l}}\Delta T_{pl}$ ,

где 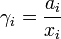$~\Delta H_{pl}$ — теплота плавления растворителя.

По осмотическому давлению раствора

Величина осмотического давления раствора может быть использована для определения активности растворителя в соответствии с соотношением:

$~\ln a_1 = - \frac{\pi\overline{V_1}}{RT}$

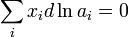где $~\pi$ — осмотическое давление, 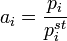$\overline{V_1}$ — парциальный молярный объём растворителя.

По распределению компонента между конденсированными фазами

Активность компонента раствора можно определить, изучая равновесное распределение его между двумя контактирующими конденсированными фазами, одна из которых — исследуемый раствор, а для другой активность или коэффициент активности уже известны. В общем случае:

$~\frac{a_i^I}{a_i^{I_{st}}}=\frac{a_i^{II}}{a_i^{II_{st}}}$

В частности, если выбор стандартного состояния компонента для фаз таков, что 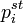$~\mu_i^{0_{I}}=\mu_i^{0_{II}}$ , это выражение принимает более простой вид:

$~a_i^I=a_i^{II}$

Экспериментально в этом методе определяют равновесные концентрации компонента или коэффициент распределения компонента между растворами.

По равновесию химической реакции с газовой фазой

При исследовании оксидных расплавов активность компонентов часто определяют, используя следующие химические реакции:

MeO + H₂ = Me + H₂O

MeO + CO = Me + CO₂

Для первой из приведенных реакций константа равновесия имеет вид:

$~K_{MeO} = \frac{p_{H_2O}\cdot a_{Me}}{p_{H_2}\cdot a_{MeO}}$

Если оксидный и металлический расплавы взаимно нерастворимы и восстанавливается индивидуальный оксид, то 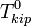$~a_{Me}=1$ , и тогда:

$~a_{MeO}=\frac{1}{K_{MeO}}\cdot\frac{p_{H_{2}O}}{p_{H_2}}$

Если металл выделяется в виде сплава с другими компонентами или растворяется в фазе-коллекторе, его активность не равна единице и формула принимает вид:

$~a_{MeO}=\frac{1}{K_{MeO}}\cdot\frac{p_{H_{2}O}}{p_{H_2}}\cdot a_{Me}$

Активность металла в сплаве здесь должна быть известна из независимых измерений.

Опытным путем в данном методе определяют отношение 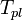$~\frac{P_{H_2O}}{P_{H_2}}$ .

Кроме того, активность оксидного компонента связана с равновесным давлением кислорода над расплавом, с учетом реакций в газовой фазе, например:

$~H_2+\tfrac{1}{2}O_2=H_2O$

или

$~CO+\tfrac{1}{2}O_2=CO_2$

Тогда можно показать, что 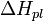$~a_{MeO} = \frac{P_{O_2}^{\tfrac{1}{2}}}{^{\tfrac{1}{2}}}$

Для сульфидных расплавов используют реакцию:

$~MeS + H_2 = Me + H_2S$

или:

$~MeS + O_2 = Me + SO_2$

По значению э. д. с. гальванического элемента

Электродвижущая сила концентрационной цепи с переносом может быть выражена следующим соотношением:

$~E = \frac{RT}{nF}\ln{\frac{{a''}_{Me}}{{a'}_{Me}}}$

Соответственно, такую цепь можно использовать для нахождения активности и коэффициента активности. В некоторых случаях побочное взаимодейтсвие электролита с электродами может приводить к невозможности определения активности компонентов по ЭДС цепи, тогда используют концентрационные цепи без переноса. Нахождение активности компонента по ЭДС концентрационной цепи без переноса — один из самых точных способов определения активности .

<<< Адсорбция

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории