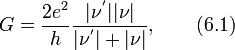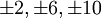Химия - Квантовый вихрь

28 февраля 2011


Оглавление:
1. Квантовый вихрь
2. Экспериментальная проверка

Квантовый вихрь — топологический дефект, который проявляется в сверхтекучей жидкости и сверхпроводниках. Безусловно, квантование циркуляции скорости в сверхпроводящих жидкостях отличается от квантования в сверхпроводниках. Но сохраняется ключевое подобие, которое состоит в топологичности дефектов, а также в том, что они квантуются. Следует отметить, что на оси квантового вихря отсутствует сверхтекучесть и сверхпроводимость. В сверхтекучей жидкости квантовый вихрь переносит угловой момент, что позволяет ей вращаться; в сверхпроводниках вихрь переносит магнитный поток.

История

Двухжидкостные уравнения Ландау, которые описывают динамику гелия-4, не совпадают с классическими уравнениями Эйлера. А это означает, что двухжидкостная теория не вытекает из законов Ньютона. Таким образом, для понимания свойств He II на микроскопическом или молекулярном уровне необходимо использовать квантовую теорию. В пользу этого также говорит и тот факт, что при таких низких температурах длина волны де Бройля

атома гелия, движущегося с тепловой скоростью, становится величиной одного порядка с межатомными расстояниями. Поэтому здесь кардинальную роль играет то, что атомы гелия-4 удовлетворяют статистике Бозе-Эйнштейна, а для понимания микроскопического поведения He II необходимо использовать первичные принципы квантовой теории. По этой причине He II называют квантовой жидкостью.

Но двухжидкостные уравнения Ландау, которые составляют фундамент описания и объяснения свойств He II, не содержат постоянной Планка, и в этом смысле они также принадлежат к классике, как и уравнения Эйлера.

Состояние проблемы с He II кардинально изменилось в 1948 году, после ключевой работы Онсагера. Ричард Фейнман и независимо Алексей Абрикосов) в 1955 году также пришли к аналогичному результату. Они выдвинули предположение, что квант действия непосредственно должен входить в макроскопическую двухжидкостную теорию Ландау с помощью введения условия квантования циркуляции скорости сверхтекучей компоненты:

где n — целое. Отсюда вытекает, что вихри сверхтекучей компоненты квантуются.

Следует отметить, что квантование циркуляции скорости похоже на условия квантования Бора-Зоммерфельда в ранней квантовой теории. Последнее условие означает, что адиабатические инварианты классического движения должны соответствовать дискретному набору состояний, то есть:

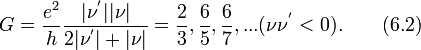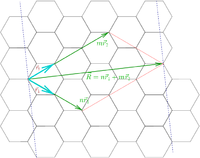где и — каноничные координаты, а интеграл берется по периоду движения.

Эти квантовые условия не выводятся из какой-то теории, а постулируются. Единственным критерием их справедливости является эксперимент.

Просмотров: 2817

<<< Квантовая точка

Квантовый провод >>>