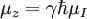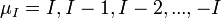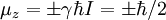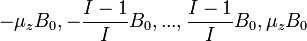Межзвёздная среда - Физические особенности

Химия - Межзвёздная среда - Физические особенности

01 марта 2011

Оглавление:
1. Межзвёздная среда
2. История открытия
3. Наблюдательные проявления
4. Физические особенности
5. Эволюция межзвёздной среды
6. Солнце и межзвёздная среда

Отсутствие локального термодинамического равновесия

В межзвёздной среде концентрация атомов мала и оптические толщи малы. Это значит, что температура излучения — это температура излучения звёзд и никак не соответствует температуре самой среды. При этом электронная и ионная температуры плазмы могут сильно отличаться друг от друга, поскольку обмен энергии при соударении происходит крайне редко. Таким образом, не существует единой температуры даже в локальном смысле.

Распределение числа атомов и ионов по населённостям уровней определяется балансом процессов рекомбинации и ионизации. ЛТР требует, чтобы эти процессы были в равновесии, чтобы выполнялось условие детального баланса, однако, в межзвёздной среде прямые и обратные элементарные процессы имеют разную природу, и поэтому детальный баланс установиться не может.

И наконец, малая оптическая толщина для жёсткого излучения и быстрых заряженных частиц приводит к тому, что энергия, выделяющаяся в какой-либо области пространства, уносится на большие расстояния. И охлаждение идёт по всему объёму сразу, а не в локальном пространстве, расширяющемся со скоростью звука в среде. Аналогично и идёт нагрев. Теплопроводность не способна передать тепло от удалённого источника и в дело вступают процессы, нагревающие большие объёмы сразу.

Однако, несмотря на отсутствие ЛТР, даже в очень разреженной космической плазме устанавливается максвелловское распределение электронов по скоростям, соответствующее температуре среды, поэтому для распределения частиц по энергиям можно пользоваться формулой Больцмана и говорить о температуре. Происходит так из-за дальнодействия кулоновских сил за довольно короткое время, гораздо меньше времени соударения между частицами.

Для описания состояния газа введём объёмный коэффициент нагревания Λ и коэффициент объёмного нагрева Γ. Тогда закон сохранения энергии элемента объёма dV с внутренней энергией E и давлением P запишется:

$\frac{dQ}{dt}=\frac{dE}{dt}+P\frac{dV}{dt}=\Gamma-\Lambda$

При тепловом равновесии dQ/dt=0, а значит равновесную температуру среды можно найти из соотношения Γ=Λ.

Механизмы нагрева

Говоря, что среда нагревается, мы подразумеваем рост средней кинетической энергии. При объёмном нагреве увеличивается кинетическая энергия каждой частицы. И каждая частица в единицу времени может увеличить свою энергию на конечную величину, а при отсутствии термодинамического равновесия, это означает, что скорость нагрева среды прямо пропорционально количеству частиц в единице объёма, то есть концентрации Γ=nG. Функция Gназывается эффективностью нагрева и рассчитывается через элементарные процессы взаимодействия и излучения.

Ультрафиолетовое излучение звёзд

Классический фотоэффект: энергия кванта уходит на ионизацию атома с произвольного уровня i и кинетическую энергию электрона. Потом электроны соударяются с различными частицами и кинетическая энергия переходит в энергию хаотического движения, газ нагревается.

Однако не все так просто. Межзвёздный газ состоит из водорода, ионизовать который можно только жёстким УФ. И основными «перехватчиками» УФ-квантов оказываются атомы примесей: железа, кремния, сера, кали и др. Они играют важную роль в установлении теплового баланса холодного газа.

Ударные волны

NGC 2736, газ, внутри остатка сверхновой в созвездии «Паруса»

Ударные волны возникают при процессах, идущих со сверхзвуковыми скоростями. Так происходит при вспышке сверхновой, сбросе оболочки, столкновения газовых облаков между собой, гравитационный коллапс газового облака и т. д. За фронтом ударной волны кинетическая энергия направленного движения быстро переходит в энергию хаотического движения частиц. Порой температура может достигать огромных значений, причём основная энергия приходится на движение тяжёлых ионов. Поначалу температура легко электронного газа значительно ниже, но постепенно благодаря кулоновским взаимодействиям ионная и электронная температура выравнивается. Если в плазме есть магнитное поле, то роль первой скрипки в выравнивании ионной и электронной температуры берет на себя турбулентность.

Проникающая радиация и космические лучи

Космические лучи и рентгеновское диффузное излучение -основные источники ионизации межзвёздной среды, а не УФ, как это можно было ожидать. Частицы космических лучей, взаимодействуя со средой, образуют электроны с очень большой энергией. Эта энергия теряется электроном, в упругих столкновениях, а также неупругих, приводящих к ионизации или возбуждению атомов и ионов. Надтепловые электроны, с энергией меньше 10 эВ теряют энергию в упругих столкновениях, нагревая газ. Такой механизм крайне эффективен при температурах < 10. При 10 характерная тепловая скорость электронов сравнивается тепловой скоростью низкоэнергетических частиц космических лучей и скорость нагрева резко уменьшается.

Ионизация и нагрев с помощью мягкого диффузного рентгена от горячего газа ничем принципиально не отличается от нагрева космическими лучами. Всё различие в скорости нагрева и в намного большем сечении фотоионизации с внутренних оболочек у рентгеновского излучения.

Жёсткое электромагнитное излучение

Осуществляется в основном вторичными электронами при фотоионизации и при комптоновском рассеянии. При этом передаваемая энергия покоящемуся электрону равна

$\Delta E=h\nu \frac{h\nu}{m_e c^2}$

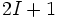для $h\nu\ll m_e c^2$ сечение рассеяние равно томсоновскому: 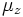$\sigma_{T}\simeq 6,65*10^{-25}$ см².

Механизмы охлаждения

Как уже говорилось, межзвёздная среда оптически тонка и имеет невеликую плотность, а раз так, то основной механизм охлаждения — это излучение фотонов. Испускание же квантов зависит с бинарными процессами взаимодействия, поэтому суммарную скорость объёмного охлаждения можно представить в виде Λ = nλ. Где функция охлаждения зависит только от температуры и химического состава.

Свободно-свободное излучение

Свободно-свободное излучение в космической плазме вызвано кулоновскими силами притяжения или отталкивания. Электрон ускоряется в поле иона и начинают излучать электромагнитные волны. Электрон начинает переходить с одной орбиты на другую, но оставаясь свободным. При этом излучается весь спектр от рентгена до радио. Выделяющаяся при этом энергия из единицы объёма внутри телесного угла в ед. времени равна:

$j_{\nu}=\frac{16}{3}^{1/2} \frac{n_{\nu}Z^{2}e^6}{m^{2}_e c^3}^{1/2} g\exp{\frac{-h\nu}{kt}}n_e n_i$

Где n_ν показатель преломления. g — множитель Гаунта, n_e и n_i — концентрация электронов и ионов соответственно. Для чисто водородной плазмы с равной концентрацией протонов и электронов коэффициент объёмного охлаждения равен:

$\Lambda_{ff} =\int\limits_{0}^{\infty}{j_{\nu}d\nu}\simeq 1.43\cdot 10^{-27} n_{e}^{2}\sqrt{T}$

Однако космическая плазма не чисто водородная, в ней есть тяжёлые элементы, благодаря большому заряду которых, увеличивается эффективность охлаждения. Для полностью ионизированной среды с нормальным космическим содержанием элементов 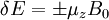$\Lambda_{ff}\approx 1.7\Lambda_{ff}$ . Этот механизм особенно эффективен для плазмы с T>10.

Рекомбинационное излучение

Радиативная рекомбинация

При радиативной рекомбинации доля кинетической энергии рекомбинирующего электрона крайне мала в энергии испускаемого фотона hν = ξ_i + m_ev (ξ_i -потенциал ионизации уровня, на который рекомбинирует электрон. Так как почти всегда 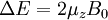$\xi_i\gg m_ev^2/2$ , то большая часть выделяющееся энергии не тепловая. Поэтому радиативная рекомбинация в общем случае малоэффективна для охлаждения газа. 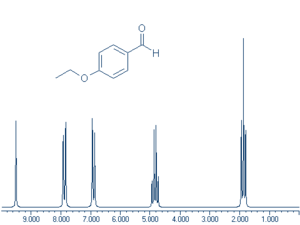Однако мощность излучения единицы объёма из-за радиативной рекомбинации для равновесной среды с Т<10 превосходит потери на тормозное излучение $\Lambda_r\approx 4\Lambda_{ff}$ .
Диэлектронная рекомбинация

Диэлектронная рекомбинация состоит из двух этапов. Сначала энергичный электрон возбуждает атом или ион так, что образуется неустойчивой ион с двумя возбужденными электронами. Далее либо электрон испускается и ион перестаёт быть неустойчивым, либо испускается фотон с энергией порядка потенциала ионизации и ион вновь становиться устойчивым. Для того, чтобы возбудить атом нужен очень быстрый электрон, с энергией выше средней. Понижая количество быстрых электронов мы понижаем среднюю энергию системы, среда охлаждается. Данный механизм охлаждения начинает доминировать над радиативной рекомбинацией при T>10 К.

Двухфотонное излучение

Возникает при запрещённых резонансных переходах с уровней $2s_{1/2}\rightarrow 1s_{1/2}$ в водороде, при этом излучается два фотона, и с 2S₀ уровня в гелии и гелиеподобных ионах с испусканием также двух фотонов. Возбуждается же эти уровни в основном за счёт электронных ударов. Суммарная энергия образующихся фотонов соответствует разности энергии между двумя уровнями, но каждый из фотонов не имеет фиксированной энергии и образуется непрерывное излучение, кое мы видим в зонах HII. Эти фотоны имеют длину волны больше чем у Лайман-альфы и уходят из среды, являясь основной причиной охлаждения горячей космической плазмы с Т=10 − 10 К.

Обратное комптоновское рассеяние

Если рассеяние фотона с энергией ε происходит на быстром электроне с энергией E = γm_ec важным становится передача энергии и импульса от электрона фотону. Лоренц-преобразование в системе электрона даёт энергию фотона γε. Воспользуемся формулой эффекта Комптона и перейдём обратно получаем ε₁˜γε. Видно, что низкочастотные кванты превращаются в кванты жёсткого излучения. Усредняя по углам скорость потерь энергии одного такого электрона в поле изотропного излучения получим

$-\left _{compt} = \frac{4}{3}\sigma_Tc\gamma^2\beta^2\int\limits_0^\infty u_{\nu}d\nu$

В случае теплового распределения электронов с концентрацией n_e и температурой T имеем < β > = < > = 3kT / m_ec. Принимая 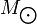$\gamma\approx 1$ . Объёмное охлаждение такой среды составит:

$\Lambda _c=-\left _{compt} n_e = \frac{4kT}{m_e c^2}\sigma_T c n_e\int\limits_0^\infty u_{\nu}d\nu$

Комптоновское охлаждение обычно доминирует в высокоионизированной и сильно нагретой плазме вблизи источников рентгеновского излучения. Благодаря ему среда не может нагреться выше 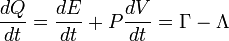$T\sim\frac{\epsilon}{4k}$ . Этот механизм был важен в ранней вселенной до эпохи рекомбинации. В обычных условиях МЗС эффектом можно пренебречь.

Ионизация электронным ударом

Если все остальные механизмы охлаждения излучательные, энергия уносится фотонами, то этот безызлучательный. Тепловая энергия расходуется на отрыв электрона и запасается в виде внутренней энергии связи ион-электрон. Потом она высвечивается при рекомбинациях.

Излучение в спектральных линиях

Основной механизм охлаждения МЗС при Т<10 K.Излучение происходит при переходах с уровней, возбужденных после электронного удара. Спектральный диапазон в котором уносится энергия определяется температурой — чем больше температура, тем более высокий уровень возбуждается, тем энергичнее излучаемый фотон и охлаждение идёт быстрее. В таблице приведены какие линии доминируют при различных температурах.

Температура К	Охлаждение в линиях
> 10	Рентгеновские линии Н и Не-подобных ионов тяжёлых элементов
2 10 — 10	Резонансные УФ-линии Не и тяжёлых до Fe
10	Линии Н
10	Запрещённые линии тяжёлых элементов
30 − 10	Далёкие ИК-линии при переходах между уровнями тонкой структуры основных термов
10	Молекулярные уровни, в основном H₂
<30	Вращательные переходы молекул СО и воды H₂O

Тепловая неустойчивость

Теперь, зная все элементарные процессы и механизмы охлаждения и нагрева мы можем записать уравнения теплового баланса в виде nG = nλ. Запишем уравнение ионизационного баланса, необходимое чтобы узнать населённость уровней. Решая, получим равновесную температуру T. Учитывая то, что вещество в межзвёздной среде крайне разряжено, то есть представляет из себя идеальный газ, подчиняющийся уравнению Менделеева-Клапейрона, найдём равновесное давление P. И обнаружим, что зависимость больше напоминает уравнение состояни газа Ван-дер-Вальса: существует область давлений, где одному значению p соответствует три равновесных эначения n. Решение на участке с отрицательной производной неустойчиво относительно малых возмущений: при давлении больше чем у окружающей среды она будет расширяться до установления равновесия при меньшей плотности, а при меньшем картина с точностью до наоборот. Это объясняет наблюдаемое динамическое равновесие разреженной межзвёздной среды и более плотных облаков межзвёздного газа.

В реальной же среде ситуация гораздо сложнее. Во-первых, существует магнитное поле, которое препятствует сжатию, если только оно не происходит вдоль линий поля. Во-вторых, межзвёздная среда находится в непрерывном движении и её локальные свойства непрерывно меняются, в ней появляются новые источники энергии и исчезают старые. Так что условие теплового равновесия может вовсе не выполняться. В-третьих, кроме термодинамической неустойчивости существуют гравитационная и магнитогидродинамическая. И это без учётов всякого рода катаклизмов в виде вспышек сверхновых, приливных влияний, проходящих по соседству галактик, или прохождения самого газа через спиральные ветви Галактики.

Запрещённые линии и линия 21 см

Отличительной особенностью оптически тонкой среды является излучение в запрещённых линиях. Запрещёнными называют линии, которые запрещены правилами отбора, то есть происходят с метастабильных уровней. Характерное время жизни электрона на этом уровне — от 10 с до нескольких суток. При высоких концентрациях частиц их столкновение снимает возбуждение и линии не наблюдаются из-за крайней слабости. При и малых плотностях интенсивность линии не зависит от вероятности перехода, поскольку малая вероятность компенсируется большим числом атомов находящихся в метастабильном состоянии. Если ЛТР нет, то заселённость энергетических уровней следует рассчитывать из баланса элементарных процессов возбуждения и деактивации.

Важнейшей запрещённой линией МЗС является радиолиния атомарного водорода 21 см. Эта линия возникает при переходе между подуровнями сверхтонкой структуры 1S_{1 / 2} уровня водорода, связанными с наличием спина у электрона и протона. Вероятность этого перехода $A_{10} = 2.9 \cdot 10^{-15}$ . Возбуждение происходит благодаря столкновению нейтральных атомов водорода. Расчёт населённости уровней даёт n₁ = n_H / 4, n₀ = 3n_H / 4. При этом объёмный коэффициент излучения:

$j_{\nu}=\frac{h\nu_{10}}{4\pi}n_1A_{10}\phi$

Где φ — профиль линии, а фактор 4π предполагает изотропное излучение.

Исследования радиолинии 21 см позволили установить, что нейтральный водород в галактике в основном заключён в очень тонком 400 пк толщиной слое около плоскости Галактики. В распределении HI отчётливо прослеживаются спиральные ветви Галактики, Зеемановское расщепление абсорбционных компонент линии у сильных радиоисточников используется для оценки магнитного поля внутри облаков.

Вмороженность магнитного поля

Вмороженность магнитного поля означает сохранение магнитного потока через любой замкнутый проводящий контур при его деформации. В лабораторных условиях магнитный поток можно считать сохраняющимся в средах с высокой электропроводностью. В пределе бесконечной электропроводности бесконечное малое электрическое поле вызвало бы рост тока до бесконечной величины. Следовательно идеальный проводник не должен пересекать магнитные силовые линии, и таким образом возбуждать электрическое поле, а напротив должен увлекать за собой линии магнитного поля, магнитное поле оказывается как бы вмороженным в проводник.

Реальная космическая плазма, далеко не идеальна и вмороженность стоит понимать в том смысле, что требуется очень большое время для изменения потока через контур. На практике это означает, что мы можем считать поле постоянным пока облако сжимается, обращается и т. д.

<<< Космическая пыль

Межзвёздные молекулы >>>

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории