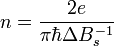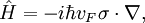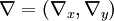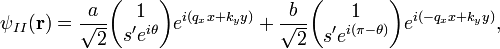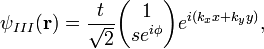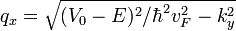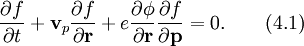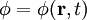Плазменные волны в графене

Химия - Плазменные волны в графене

01 марта 2011

Как и в обычных полупроводниках в графене электронно-дырочный газ можно рассматривать как плазму и соответственно ставить вопрос о том какие волны могут наблюдаться в твёрдом теле. Благодаря отличию закона дисперсии от параболического ожидается, что и свойства волн будут другими. Плазменные волны в ДЭГ в графене теоретически рассматривались в работе .

Вывод

Кинетическое уравнение для электронов в графене в бесстолкновительном приближении запишется в виде

$\frac{\partial f}{\partial t}+\mathbf{v}_p\frac{\partial f}{\partial \mathbf{r}}+e\frac{\partial \phi}{\partial \mathbf{r}}\frac{\partial f}{\partial \mathbf{p}}=0.\qquad$

Здесь функция распределения электронов 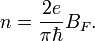$f=f$ зависит от координат, импульсов и времени. 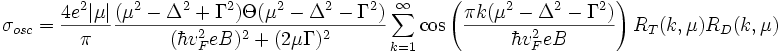$\phi=\phi$ — потенциал создаваемый ДЭГ. Так как графен двумерная система, то вектор импульса имеет только две координаты 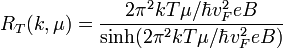$\mathbf{p}=$ . Также скорость электронов задаётся формулой 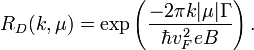$\mathbf{v}_{\mathbf{p}}=v_F\frac{\mathbf{p}}{p}$ , где $p=|\mathbf{p}|$ .

Уравнение Пуассона, которое связывает концентрацию и распределение потенциала в графене, можно свести к уравнению

$\frac{V_g-\phi}{W_g}=\frac{4\pi e}{\varepsilon}\Sigma,\qquad$

где V_g — приложенное напряжение на затворе, которым можно управлять концентрацией, W_g — толщина диэлектрика с диэлектрической проницаемостью 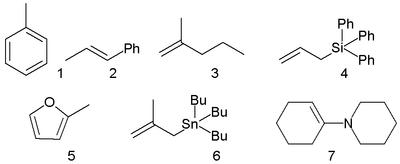$\varepsilon$ , а концентрация электронов Σ задаётся по формуле

$\Sigma=\frac{g_sg_v}{^2}\int{d^2\mathbf{p}f},\qquad$

которая аналогична выражению.

Совместное решение уравнений и в виде плоских даёт ответ на вопрос о плазменных волнах в графене.

Решение уравнения ищется в виде

$f=f_0+\delta fe^{i},\qquad$

где к равновесной функции распределения добавляется малая поправка в виде плоской волны. Потенциал также является малым возмущением

$\phi=\delta\phi e^{i}.\qquad$

При подстановки решений и в и приходим к уравнениям на δf и δφ с точностью до первого порядка малости

$\left\delta f=-ek\frac{\partial f_0}{\partial p_x}\delta\phi,\qquad$

$\delta\phi=-\frac{2eW_g}{\pi\varepsilon\hbar^2}\int{d^2\mathbf{p}f}.\qquad$

Эти уравнения легко решаются если электронный газ вырожден, то есть 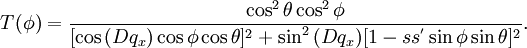$k_BT\ll E_F$ . Для ω > v_Fk получим линейное дисперсионное соотношение для плазменных волн в графене

$\omega=\frac{kv_F}{\sqrt{1-\left^2}}=ks,\qquad$

где

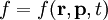$\alpha=\sqrt{\frac{4g_sg_ve^3W_gV_g}{\varepsilon\hbar^2v_F^2}}.\qquad$ .

Фазовая и групповая скорости равны

$s=\frac{v_F}{\sqrt{1-\left^2}}.\qquad$

Учёт конечных температур и, соответственно, термически возбуждённых дырок рассмотрено в работе .

<<< Парадокс Клейна (графен)

Подвешенный графен >>>

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории