Химия - Теорема Редфилда Пойа
01 марта 2011Оглавление:
1. Теорема Редфилда Пойа
2. Теорема Редфилда—Пойа
Теорема Редфилда — Пойа — классический результат перечислительной комбинаторики.
Впервые эта теорема была получена и опубликована Редфилдом в 1927 году, но работа была сочтена весьма специальной и осталась незамеченной. Пойа независимо доказал то же самое в 1937 году, но оказался куда более успешным популяризатором — так, например, в первой же публикации он показал применимость этого результата к перечислению химических соединений.
Вводные определения
Пусть заданы два конечных множества X и Y, а также весовая функция 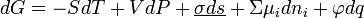 . Положим n = | X | . Без потери общности можно считать, что
. Положим n = | X | . Без потери общности можно считать, что  .
.
Рассмотрим множество функций  . При этом вес функции f определяется как
. При этом вес функции f определяется как
 .
.
Пусть на множестве X действует некоторая подгруппа A симметрической группы Sn. Введем отношение эквивалентности на F
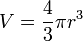 для некоторого
для некоторого 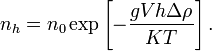 .
.
Класс эквивалентности f обозначим через и будем называть орбитой f. Так как веса эквивалентных функций совпадают, то можно определить вес орбиты как w = w.
Пусть
 — число элементов Y веса k;
— число элементов Y веса k; — число орбит веса k;
— число орбит веса k; и
и  — соответствующие производящие функции.
— соответствующие производящие функции.
Цикловой индекс
Цикловой индекс подгруппы A симметрической группы Sn определяется как многочлен от n переменных 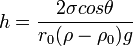
где jk — число циклов длины k в перестановке a.
Просмотров: 2820
|
|
