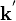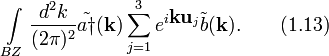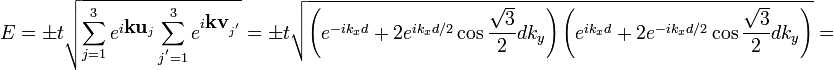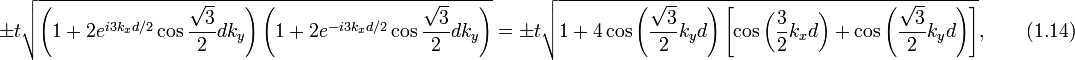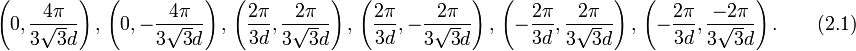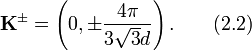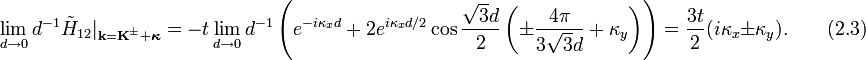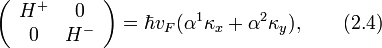Уравнение Дирака для графена - Произвольный поворот системы координат

Химия - Уравнение Дирака для графена - Произвольный поворот системы координат

01 марта 2011

Оглавление:
1. Уравнение Дирака для графена
2. Вывод
3. Произвольный поворот системы координат

Поскольку закон дисперсии не должен зависеть в низкоэнергетическом приближении от ориентации кристаллической решётки относительно системы координат, а уравнение Дирака для графена не обладает таким свойством, то возникает вопрос об общем виде уравнения Дирака при повороте системы координат. Ясно, что единственное различие между уравнениями Дирака в заданной системе координат и повёрнутой на угол α системой координат, при условии сохранения закона дисперсии, заключается в добавке фазовых факторов. Вычисления приводят к гамильтониану для свободных частиц вида

$H_{\pm}=-i\hbar v \left( \begin{array}{cc} 0 & e^{\pm i\alpha} \\ e^{\mp i\alpha} & 0 \\ \end{array} \right),\qquad$

из которого можно получить все уравнения, которые используются в литературе.

В литературе встречается гамильтониан в виде

$H_{\pm}=-i\hbar v \left( \begin{array}{cc} 0 & \pm\partial_x-i\partial_y \\ \pm\partial_x+i\partial_y & 0 \\ \end{array} \right),\qquad$

который получается из если взять угол α = − π / 2.

Решение уравнения Дирака

Рассмотрим гамильтониан для одной долины

$H_{+}=-i\hbar v\begin{pmatrix} 0 & i\frac{\partial}{\partial x}+ \frac{\partial}{\partial y}\\ -i\frac{\partial}{\partial x}+\frac{\partial}{\partial y} & 0 \end{pmatrix}.\qquad$

Волновая функция представляется в виде спинора состоящего из двух компонентов

$\Psi=\begin{pmatrix} \phi\\ \chi\end{pmatrix}.\qquad$

Эта функция удовлетворяет следующему уравнению для свободных частиц

$\left\{\begin{matrix} -i\hbar v\left=E\phi & \\ -i\hbar v\left=E\chi & \end{matrix}\right.\qquad$

Подставляя второе уравнение в первое получим волновое уравнение

$\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}=-\frac{E^2}{\hbar^2v^2}\phi,\qquad$

решением которого будет плоская волна

$\phi=\frac{1}{\sqrt{2}}e^{ik_xx+ik_yy}.\qquad$

Собственные значение имеют вид непрерывного линейного спектра

$E=\pm\hbar vk_F=\pm\hbar v\sqrt{k_x^2+k_y^2}.\qquad$

Вторую компоненту волновой функции легко найти подставив найденное решение во второе уравнение

$\chi=-i\frac{\hbar v \left}{E}\frac{1}{\sqrt{2}}e^{ik_xx+ik_yy}=-ie^{i\theta}\frac{\hbar vk_F }{E}\frac{1}{\sqrt{2}}e^{ik_xx+ik_yy}.\qquad$

Поэтому волновая функция для K долины запишется в виде

$\Psi=\frac{1}{\sqrt{2}}\begin{pmatrix} 1\\-ie^{i\theta}\frac{\hbar vk_F}{E}\end{pmatrix}e^{ik_xx+ik_yy}.\qquad$

<<<

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории