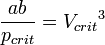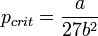Уравнение Вигнера-Поляни

Химия - Уравнение Вигнера-Поляни

01 марта 2011

Оглавление:
1. Уравнение Вигнера-Поляни
2. Интегральная форма уравнения Вигнера-Поляни

Уравнение Вигнера-Поляни - дифференциальное уравнение описывающие кинетику термической десорбции молекул, адсорбированных на поверхности твердого тела. Названо по имени ученых, применивших данный тип уравнений для описания процессов десорбции с твердой поверхности.

$-\frac{d\theta }{dt}=k{\theta }^{n}=A{e}^{-\frac{{E}_{a}}{RT}}{\theta }^{n}$

где θ - поверхностная концентрация адсорбированных молекул, или степень заполнения поверхности, k - константа скорости десорбции, А - предэкспоненциальный множитель, E_a-энергия активации, R -универсальная газовая постоянная , Т - термодинамическая температура, n - порядок процесса

Термопрограммированная десорбция

Очень часто, уравнение Вигнера-Поляни применяют в случае линейного повышения температуры:

T = T_o + βt, где β-скорость нагрева

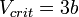$dt=\frac{dT}{\beta }$ - поставляем в исходное уравнение

$-\frac{d\theta }{dT}=\frac{A}{\beta }{e}^{-\frac{{E}_{a}}{RT}}{\theta }^{n}$

Записанное в такой форме уравнение, называют уравнением Вигнера-Поляни для линейного нагрева

<<< Уравнение Ван-дер-Ваальса

Уравнение Нернста >>>

Химики
Бытовая химия
Химические вещества
Химические законы и уравнения
История химии
Лабораторная техника

Химическое машиностроение
Награды в области химических наук
Химическая номенклатура
Химическое образование
Химические общества
Химическая промышленность

Разделы химии
Химические реакции
Химические свойства
Химическая связь
Химические системы
Химические теории