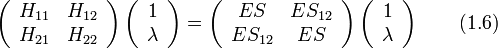Химия - Зонная структура графена
01 марта 2011Зонная структура графена рассчитана в статье . На внешней оболочке атома углерода находится 4 электрона, три из которых образуют sp² гибридизированные связи с соседними атомами в решётки, а оставшийся электрон находится в 2pz состоянии. В нашем рассмотрении он отвечает за образование энергетических зон графена.
Вывод
| Фундаментальные понятия |
|---|
| Зонная структура · Уравнение Дирака · Киральность · Гексагональная решётка · Волновая функция · Точка электронейтральности · Видимость графена · Фаза Берри |
| Получение и технология |
|---|
| Получение графена · Механическое отшелушивание · Химическое расщепление графита · Рост графеновых плёнок · Подвешенный графен · Верхний затвор |
| Применения |
|---|
| Графеновый полевой транзистор Графеновые наноленты |
| Транспортные свойства |
|---|
| Электроны и дырки · Проводимость · Фононы· Парадокс Клейна · Линза Веселаго · 1/f · Дробовой шум Случайный телеграфный сигнал · p — n переход · Ферми жидкость |
| Магнитное поле |
|---|
| Магнетосопротивление · Осцилляции Шубникова — деГааза · КЭХ · Спиновый квантовый эффект Холла · ДКЭХ · Осцилляции Вейса · Магнетоэкситоны · Сверхпроводимость · Слабая локализация · Эффект Ааронова — Бома |
| Оптика графена |
|---|
| Рамановское рассеяние света |
| Известные учёные |
|---|
| Андре Гейм · Константин Новосёлов |
В приближении сильно связанных электронов полная волновая функция всех электронов кристалла запишется в виде суммы волновых функций электронов из разных подрешёток
где коэффициент λ — параметр, который определяется из системы уравнений. Входящие в уравнение волновые функции φ1 и φ2, которые по смыслу означают амплитуды волновых функций на определённой подрешётке кристалла, запишутся в виде суммы волновых функций отдельных электронов в различных подрешётках кристалла
Здесь  и
и 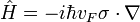 — радиус-векторы направленные на узлы кристаллической решётки, а
— радиус-векторы направленные на узлы кристаллической решётки, а  и
и  — волновые функции электронов, локализованных вблизи этих узлов. В приближении сильно связанных электронов мы можем пренебречь перекрытием волновых функций соседних атомов.
— волновые функции электронов, локализованных вблизи этих узлов. В приближении сильно связанных электронов мы можем пренебречь перекрытием волновых функций соседних атомов.
Теперь подставив в уравнение Шрёдингера Hψ = Eψ нашу волновую функцию получим для энергетического спектра носителей и неизвестного параметра λ следующую систему уравнений
- H11 + λH12 = ES + ES12λ

или в матричном виде

где используются следующие обозначения для интегралов
Которую можно решить относительно E.
Здесь можно сделать некие упрощения
- S = N,
- H11 = H22,
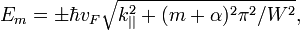
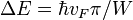
где N — число элементарных ячеек в кристалле. С этими равенствами мы приходим к уравнению
Это уравнение мы тоже упростим, избавившись от первого слагаемого, которое соответствует некой постоянной энергии и малому изменению энергии по сравнению со вторым членом, отвечающим интегралу перекрытия волновых функций соседних атомов из той же подрешётки. Другими словами — взаимодействию волновой функции центрального атома с волновыми функциями атомов, расположенных на красной окружности. Нас будет интересовать только особенность спектра связанного со вторым слагаемым, которое зависит от интегралов перекрытия ближайших атомов из разных подрешёток и. Энергетический спектр запишется в виде
Интеграл перекрытия можно представить в виде
где 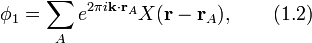 — радиус-вектор направленный в позиции ближайших соседей. Для величины
— радиус-вектор направленный в позиции ближайших соседей. Для величины 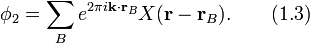 после подставления волновых функций и в выражение получим
после подставления волновых функций и в выражение получим
Откуда после некоторых упрощений и используя координаты для ближайших соседей получим
В итоге приходим к интересующему нас энергетическому спектру вида
где знак «+» соответствует электронам, а «-» —дыркам.
Просмотров: 1837
|
|







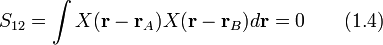
![H_{12}^{\,'}=-\gamma_0\left]}+2\cos{\pi k_ya}\exp{}\right).\qquad](/img/14640.png)